Progressão Aritmética

☰

Progressão Aritmética

Progressão Aritimética

Notações

Neste material usaremos as seguintes notações:
N: conjunto dos números naturais.

N = {1, 2, 3, . . . , n, . . .}

R, conjunto dos números reais.
⇒, sı́mbolo de implicação lógica.
A expressão A ⇒ B lê-se: “A implica B”. Por exemplo x ∈ N ⇒ x ∈ R.
⇔, sı́mbolo de equivalência lógica.

Definição. (Sequência)

Uma sequência de números reais é uma função x : N → R, que associa a cada número natural n um número real $x_{n}$ , chamado o n-ésimo termoda sequência.

Escreve-se ( $x_{1}$ , $x_{2}$ , . . ., $x_{n}$ , . . .) ou ( ${x_{n})}_{n ∈ N}$ ou simplesmente $x_{n}$ , para indicar a sequência cujo n-ésimo termo é $x_{n}$

Exemplo 1

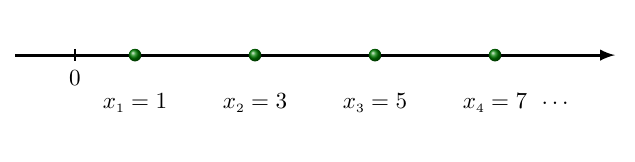
A sequência (1, 3, 5, . . . , $x_{n}$ , . . .) é a imagem da função x : N → R, definida por $x_{n}$ = 2n − 1.

Exemplo 2

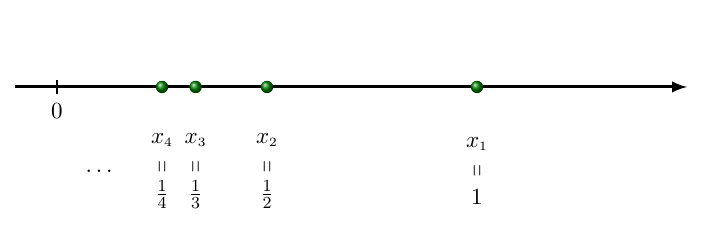
A sequência (1, $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{4}$ , . . ., $x_{n}$ ) é a imagem da função x : N → R, definida por $x_{n}$ = $\frac{1}{n}$

Definição. (Progressão aritmética)

Uma progressão aritmética é uma sequência na qual a diferença entre cada termo e o termo anterior é constante. Essa diferença constante é chamada de razão da progressão e representada pela letra r.

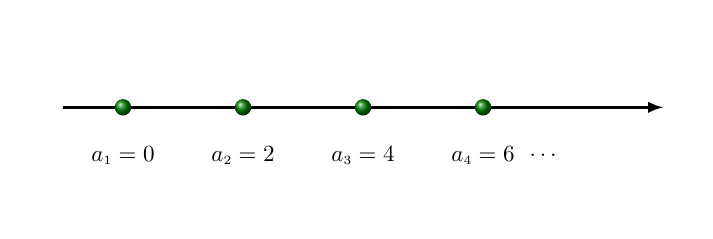
Exemplo 1

A sequência (0, 2, 4, 6, ...) é uma progressão aritmética cuja razão vale 2. De fato,

$a_{2}$ - $a_{1}$ = 2 - 0 = 2
$a_{3}$ - $a_{2}$ 4 - 2 = 0
$a_{4}$ - $a_{3}$ = 6 - 4 = 2

.
$a_{n-1}$ - $a_{n}$ = 2

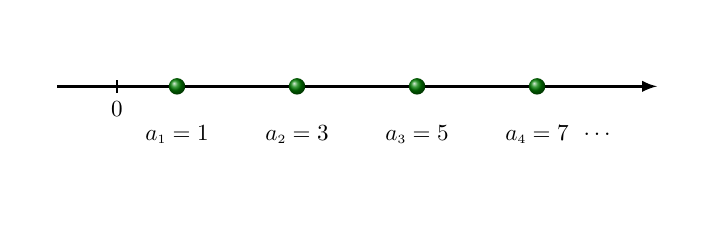
Exemplo 2

A sequência (1, 3, 5, 7, 9, 11, ...) é uma progressão aritmética cuja razão vale 2. De fato,

$a_{2}$ - $a_{1}$ = 3 - 1 = 2
$a_{3}$ - $a_{2}$ 5 - 3 = 0
$a_{4}$ - $a_{3}$ = 9 - 5 = 2
.
$a_{n-1}$ - $a_{n}$ = 2

Relação entre dois termos quaisquer de uma P.A.

Seja ( $a_{1}$ , $a_{2}$ , . . ., $x_{m}$ , . . . $x_{n}$ , . . .) uma progressão aritmética de razão r. Então

$a_{2}$ - $a_{1}$ = r
$a_{3}$ - $a_{2}$ = r
.
$a_{m}$ - $a_{m-1}$ = r
.
$a_{n}$ - $a_{n-1}$ = r

Reescrevendo as equações acima, obtemos:

$a_{2}$ = $a_{1}$ + r = $a_{1}$ + (2 - 1)r
$a_{3}$ = $a_{2}$ + r = $a_{1}$ + r + r = $a_{1}$ + 2r = $a_{1}$ + (3 - 1)r
$a_{4}$ = $a_{3}$ + r = $a_{1}$ + 2r + r = $a_{1}$ + 3r = $a_{1}$ + (4 - 1)r
.
$a_{m}$ = $a_{1}$ + (m - 1)r
.
$a_{n}$ = $a_{1}$ + (n - 1)r

Observe que:

$a_{m}$ = $a_{1}$ + (m - 1)r ⇔ $a_{1}$ = $a_{m}$ + (1 - m)r

Assim,

$a_{n}$ = $a_{1}$ + (n - 1)r
= $a_{m}$ + (1 - m)r + (n - 1)r
= $a_{m}$ + r - mr + nr - r
= $a_{m}$ + (n − m)r

Portanto,

$a_{n}$ = $a_{m}$ + (n - m)r (1)

Exemplo 3

Em uma prograssão aritmética, o quinto termo vale 30 e o vigéssimo termo vale 50. Quanto vale o oitavo termo dessa progressão.

Solução.

Veja uma interpretação geométrica do problema na figura abaixo.

Solução.

Note que $a_{5}$ = 30 e $a_{20}$ = 50. Pela equação (1), obtemos

$a_{20}$ = $a_{5}$ + (20 - 5)r
50 = 30 + 15r
20 = 15r
r = $\frac{20}{15}$
r = $\frac{4}{3}$

Usando novamente a equação (1), obtemos:

$a_{8}$ = $a_{5}$ + (8 - 5)r
$a_{8}$ = 30 + 3 x $\frac{4}{3}$
$a_{8}$ = 30 + 4
$a_{8}$ = 34

Portanto, o oitavo termo dessa progressão é igual a 34.

Progressão Geométrica

Definição. (Progressão geométrica)

Uma progressão geométrica é uma sequência na qual é constante o quociente da divisão de cada termo pelo termo anterior. Esse quociente constante é chamado de razão da progressão e é representado pela letra q.

Exemplo 1

A sequência (2, 6, 18, 54, . . .) é uma progressão geométrica cuja razão vale 3. De fato,

$\frac{a2}{a1}$ = $\frac{6}{2}$
$\frac{a3}{a2}$ = $\frac{18}{6}$
$\frac{a4}{a3}$ = $\frac{54}{18}$
.
$\frac{an}{an-1}$ = 3

A sequência (128, 32, 8, 2,. . .) é uma progressão geométrica cuja razão vale $\frac{1}{4}$ . De fato,

$\frac{a2}{a1}$ = $\frac{32}{128}$
$\frac{a3}{a2}$ = $\frac{8}{32}$
$\frac{a4}{a3}$ = $\frac{2}{8}$
.
$\frac{an}{an-1}$ = $\frac{1}{4}$

Em uma progressão geométrica ( $a_{1}$ , $a_{2}$ , $a_{3}$ , . . .), para avançar um termo basta multiplicar pela razão; para avançar dois termos, basta multiplicar duas vezes pela razão, e assim por diante.

Relação entre dois termos quaisquer de uma P.G

( $a_{1}$ , $a_{2}$ , . . ., $a_{m}$ , . . . $a_{n}$ , . . .), uma progressão geométrica de razão q.
Então

$\frac{a2}{a1}$ = q
$\frac{a3}{a2}$ = q
$\frac{a4}{a3}$ = q
.
$\frac{am}{am-1}$ = q
.
$\frac{an}{an-1}$ = q