Geometria Plana

Introdução

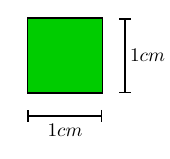
Nosso objetivo ao longo desse material é encontrar fórmulas que expres- sem as áreas de algumas figuras planas através de suas dimensões. Para tanto, nosso ponto de partida é um quadrado unitário: por definição, dizemos que a área de um quadrado de lado 1cm é igual a 1cm². (lê-se: um centı́metro quadrado).

No restante desse material, utilizamos a definição acima para deduzir fórmulas para as áreas de alguns polı́gonos convexos.

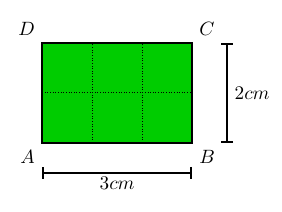
Considere, por exemplo, um retângulo cujos lados medem 2cm e 3cm. A partir de um dos vértices do retângulo, podemos traçar, a cada centı́metro, segmentos de retas perpendiculares aos lados, de modo que o retângulo fique dividido em 2 x 3 = 6 quadrados de lado 1cm (veja a figura abaixo). Desse modo, a área do retângulo é igual a 2 x 3 = 6cm².

O argumento utilizado para calcular a área do retângulo acima pode ser facilmente estendido para calcular a área de qualquer retângulo cujos lados tenham, por medidas, quantidades inteiras de centı́metros: se os lados de um retângulo medem m e n centı́metros, com m e n inteiros, então a sua área é igual a m x n cm². De fato, argumentando como no exemplo acima, podemos facilmente particionar o retângulo em m x n quadrados unitários.

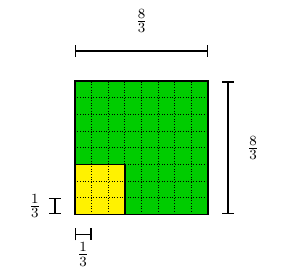
Calculemos, agora, a área do quadrado desenhado na figura a seguir, cujo lado mede $\frac{8}{3}$ cm. Veja que podemos dividir o quadrado unitário (pintado de amarelho) em 9 quadradinhos menores de lado $\frac{1}{3}$ Sendo assim, a área de cada um desses quadradinhos menores deve ser igual $\frac{1}{9}$ = ( $\frac{1}{3}$ )² cm². Por outro lado, traçando retas perpendiculares aos lados, podemos dividir o quadrado de lado $\frac{8}{3}$ em 64 quadradinhos de lado $\frac{1}{3}$ Portanto, concluı́mos que a área do quadrado de lado $\frac{8}{3}$ cm deve ser igual (em cm2 ) a

64 x $\frac{1}{9}$ = $\frac{64}{9}$ = ( $\frac{8}{3}$ )².

Adaptando o argumento acima ao caso de retângulos, podemos mostrar sem dificuldade que a área de qualquer retângulo cujos lados têm medidas em centı́metros dadas pelos números racionais $\frac{m}{n}$ e $\frac{p}{q}$ é igual (em cm²)

$\frac{m}{n}$ x $\frac{p}{q}$

Em retângulos cujos lados possuem medidas irracionais (em cm), a ideia é aproximar (tanto quanto se queira) esses números irracionais por números racionais e concluir que, ainda neste caso, temos que a área é dada (em cm²) pelo produto das medidas dos lados. Dessa forma, concluı́mos que:

A área de um retângulo de lados a e b é igual a ab.

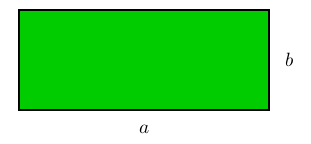
Como caso particular da fórmula acima (fazendo a = b = l) temos que:

A área de um quadrado de lado l é igual a l² .

É importante observar que as fórmulas deduzidas acima, para a área de um quadrado e um retângulo, permanecem válidas independentemente da unidade de comprimento utilizada para medir seus lados. Por exemplo, se chamarmos de unitário um quadrado de lado igual a 1m, e dissermos que sua área é igual a 1m² (lê-se: metro quadrado), então a área de um quadrado de lado (em m) igual a l será (em m²) igual a l² , ao passo que a área de um retângulo de lados (em m) iguais a a e b será (em m²) igual a ab.

Nesse sentido, o único ponto relevante é como expressar em cm² uma área dada em m², ou vice-versa. Para fazer isso, basta observar que, tomando um quadrado de lado igual a 1m e dividindo cada lado em 100 partes iguais, particionamos o quadrado em 100² quadrados de lados iguais a 1cm cada. Então, calculando áreas, concluı́mos que

1m² = 100²cm².

Calcularemos, agora, a área do paralelogramo ABCD, de base b e altura h, desenhado na figura abaixo:

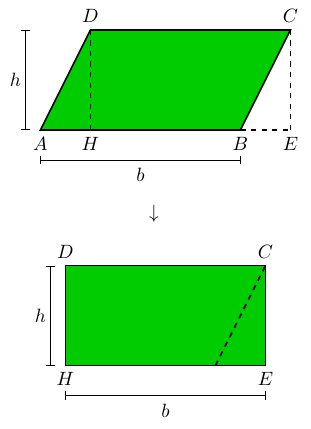
Consideremos (veja a parte de baixo da figura) a reta perpendicular ao lado CD passando por C e sua interseção E com o prolongamento do lado AB; como AB e CD são paralelos, AE e CE também são perpendiculares. Além disso, denotemos por H o pé da perpendicular ao lado AB passando pelo ponto D.
Afirmamos que os triâgulos AHD e BEC são congruentes. De fato, como DCEH é um retângulo, temos

AB = CD = EH e, daı́,
AH = AB − HB
= HE − HB
= BE;

também, AD = BC, pois são lados opostos de um paralegramo, e AHD = BEC = 90°. A congruência decorre, portanto, pelo caso especial CH, de congruência de triângulos retângulos.
Assim, escrevendo A(F) para denotar a área de uma figura F, concluı́mos que A(AHD) = A(BEC), de forma que

A(ABCD) = A(AHD) + A(HBCD)
= A(BEC) + A(HBCD)
= A(HECD)
= HE x h
= AB x h
= bh.

Em resumo,

A área de um paralelogramo de base b e altura h é bh.

Passamos, agora, ao cálculo da área de um triângulo ABC de base AB = b e altura h, mostrado em verde na figura abaixo.

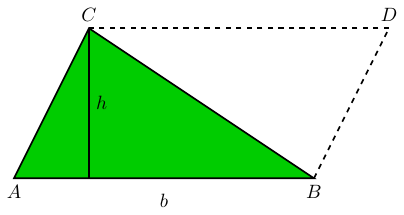
Considere o ponto D tal que ABDC é um paralelogramo. Então, a base de tal paralelogramo mede b e sua altura mede h, de sorte que sua área é igual a bh.
Mas, observe que os triângulos ABC e DCB são congruentes pelo caso LLL, pois AB = DC e AC = DB (por serem pares de lados opostos de um paralelogramo) e o lado BC é comum a ambos. Portanto, temos:

A(ABDC) = A(ABC) + A(DCB) = 2A(ABC)

e, daı́,

A(ABC) = $\frac{1}{2}$ A(ABDC) = $\frac{1}{2}$ bh.

Em resumo, concluı́mos que

A área de um triângulo de base b e altura h é $\frac{1}{2}$ bh.

Área de losangos

Como aplicação da fórmula para a área de triângulos, examinemos o caso dos losangos. Observando o losango na figura abaixo, vemos que suas diagonais o dividem em quatro triângulos retângulos congruentes. De fato, como diagonais se intersectam ao meio e os lados do losango têm todos a mesma medida, a congruência entre os quatro triângulos segue do caso LLL; logo, todos os ângulos no ponto de interseção das diagonais são retos.

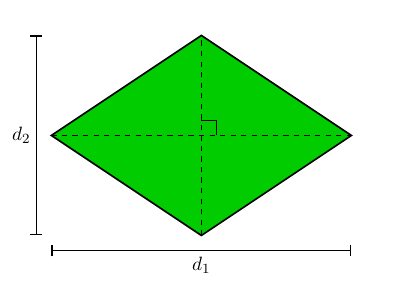
Se denotarmos as medidas das diagonais do losango por $d_{1}$ $d_{2}$ um desses triângulos retângulos tem catetos de medidas $\frac{d_{1}}{2}$ e $\frac{d_{2}}{2}$ . Como a área de um triângulo retângulo de catetos b e c é dada por $\frac{1}{2}$ bv, temos que

$\frac{1}{2}$ x $\frac{d_{1}}{2}$ x $\frac{d_{2}}{2}$ = $\frac{1}{8}$ $d_{1}$ $d_{2}$ .

Por fim, somando as áreas dos quatro triângulos, segue que o losango tem área igual a

4 x $\frac{1}{8}$ $d_{1}$ $d_{2}$ = $\frac{1}{2}$ $d_{1}$ $d_{2}$ .

Área de trapézios

Já em relação ao trapézio da próxima figura, cujas bases paralelas medem B e b e cuja altura mede h, traçando uma de suas diagonais o dividimos em dois triângulos, um de base B e altura h e outro de base b e altura h.

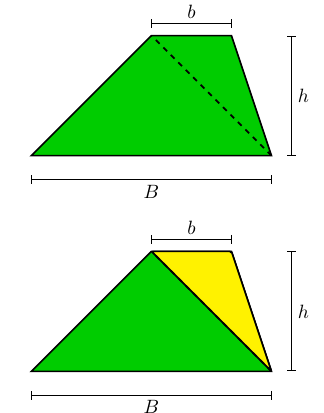
Portanto, a área do trapézio é dada por

$\frac{B x h}{2}$ + $\frac{b x h}{2}$ = $\frac{Bh + bh}{2}$ = $\frac{(B + b) x h}{2}$

Agora, apresentaremos uma fórmula para o cálculo da área de polı́gonos regulares em função do apótema e do perı́metro do polı́gono. Inicialmente, considere o triângulo equilátero ABC de lado l e apótema $a_{3}$ , inscrito em um cı́rculo de centro O e raio R (veja a figura abaixo).

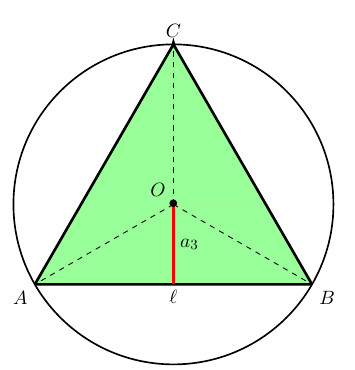
Como a figura sugere, podemos dividir o triângulo em três triângulos congruentes, OAB, OAC e OBC, todos com área igual a $\frac{1}{2}$ l x $a_{3}$ Então, a área do triângulo equilátero ABC pode ser calculada por

A(ABC) = 3 x $\frac{l xa_{3}}{2}$
= $\frac{3 x l xa_{3}}{2}$
= $\frac{3 xp_{3}xa_{3}}{2}$
= $\frac{p_{3}xa_{3}}{2}$

em que p3 é o semiperı́metro do triângulo ABC.
Para expressarmos a área de ABC de outra maneira útil, comece observando que ABO b = 30°. Então,

$\frac{\frac{a_{3}}{l}}{2}$ ⇒ $\frac{\sqrt{3}}{3}$ = $\frac{{2a}_{3}}{l}$ ⇒ $a_{3}$ = $\frac{\sqrt{3l}}{6}$

Continuando, analisemos o caso de um hexágono regular inscrito num cı́rculo de raio R, desenhado na figura a seguir:

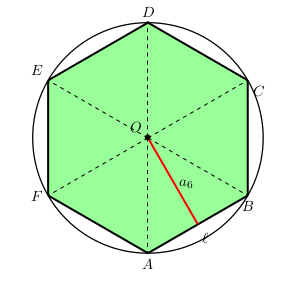
Podemos dividir o hexágono em seis √ triângulos equiláteros de lado l, os quais todos têm áreas iguais a $\frac{l² \sqrt{3}}{4}$ Portanto, a área do hexágono ABCDEF é dada por

A(ABCDEF) = 6 x $\frac{l² \sqrt{3}}{4}$ = $\frac{3 \sqrt{3}}{2}$ l².

De outro modo, observe que cada um dos seis triângulos equiláteros nos quais o hexágono foi dividido tem altura igual a a 6 , o apótema do hexágono. Portanto, a área do hexágono ABCDEF é igual à soma das áreas dos seis triângulos:

A(ABCDEF) = 6 x $\frac{l xa_{6}}{2}$ = $\frac{6l x a_{6}}{2}$ $p_{6}$ $a_{6}$