Geometria Analítica

A Geometria Analı́tica baseia-se na ideia de representar os pontos da reta por números reais, os pontos do plano por pares ordenados de números reais e os pontos do espaço por ternos ordenados de números reais. Dentro dessa concepção, as linhas e as superfı́cies, no plano e no espaço, são descritas por meio de equações. Isto permite tratar algebricamente muitas questões geométricas e, reciprocamente, interpretar de forma geométrica certas situações algébricas. A interconexão entre Geometria e Álgebra resultante desse ponto de vista foi responsável por extraordinários progressos na Matemáttica e suas aplicações.

No que se segue, apresentaremos as noções básicas de Geometria Analı́tica, enfatizando seus aspectos mais relevantes para um estudo in- trodutório. Admitiremos conhecidos os fatos mais elementares da Geometria como, por exemplo, que por dois pontos dados passa uma, e somente uma, reta; que por um ponto dado fora de uma reta passam uma única paralela e uma única perpendicular a essa reta, etc.

Coordenadas na Reta

Admitimos fixada, de uma vez por todas, uma unidade de comprimento. Dados os pontos A, B quaisquer, o comprimento do segmento de reta AB chama-se a distância entre os pontos A e B. Escrevemos d(A, B) ou AB para indicar essa distância, que é um número real.

Convencionaremos pôr d(A, A) = 0. Se A 6= B, tem-se d(A, B) > 0. Além disso, vale

d(A, C) + d(C, B) = d(A, B)

se, e somente se, o ponto C pertence ao segmento de reta AB. É claro também que d(A, B) = d(B, A).

A noção de distância permite introduzir coordenadas sobre uma reta, ou seja, representar os pontos da reta por meio de números reais. Para fazer isto, será necessário orientar a reta e escolher um dos seus pontos como origem.
Seguem-se os detalhes desse procedimento.

Definição (Reta orientada).

Uma reta diz-se orientada quando sobre ela se escolheu um sentido de percurso, chamado positivo; o sentido inverso chama-se negativo.

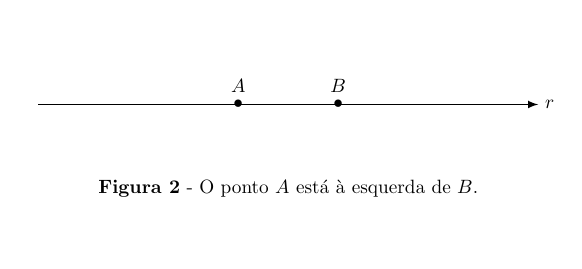
Numa reta orientada, diz-se que o ponto B está à direita do ponto A (portanto A está à esquerda de B) quando o sentido de percurso de A para B é positivo.

Definição (Eixo).

Um eixo é uma reta orientada na qual se fixou um ponto O, chamado a origem.

Todo eixo E pode ser posto, de modo natural, em correspondência biunı́voca com o conjunto R dos números reais, do seguinte modo:

A origem O do eixo faz-se corresponder o número zero.
A cada ponto X de E situado à direita de O corresponde o número real positivo x = d(O, X) = distância de X à origem = comprimento do segmento de reta OX.
Aos pontos situados à esquerda de O correspondem números reais ne- gativos, cujos valores absolutos medem as distâncias desses pontos à origem.

Portanto, a cada ponto X no eixo E corresponde o número real x = d(O, X) se X está à direita de O e x = −d(O, X) se X está à esquerda de O.

O número real x, que corresponde ao ponto X do eixo E da maneira acima indicada, chama-se a coordenada desse ponto. Reciprocamente, para cada número real x existe um (único) ponto X em E cuja coorde- nada é x.

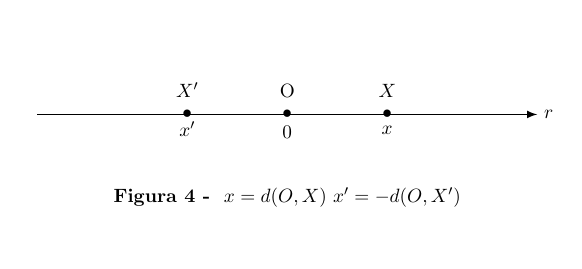
Se x e y são respectivamente as coordenadas dos pontos X e Y do eixo E então tem-se x < y se, e somente se, X está à esquerda de Y . Além disso, tem-se

d(X, Y ) = |x − y|.

A importante igualdade d(X, Y ) = |x − y| se demonstra usando (além da relação evidente d(A, B) = d(B, A)) o fato de que se A, B, C são pontos de uma reta tais que C está situado entre A e B então

d(A, B) = d(A, C) + d(C, B).

Com efeito, dados os pontos X e Y sobre o eixo E, com coordenadas respectivas x e y, sem perda de generalidade podemos supor que X esteja à esquerda de Y . Então há 3 casos possı́veis:

O está entre X e Y (logo x < 0 < y);

Y está entre X e O (logo x < y < 0);

X está entre O e Y (logo 0 < x < y).

No primeiro caso, tem-se

d(X, Y) = d(X, O) + d(O, Y ) = −x + y = |x − y|.

No segundo caso,

d(O, X) = d(O, Y) + d(Y, X),

ou seja, −x = −y + d(X, Y), donde

d(X, Y ) = y − x = |x − y|.

Finalmente, no terceiro caso,

d(O, Y) = d(O, X) + d(X, Y),

isto é, y = x + d(X, Y ) , donde

d(X, Y) = y − x = |x − y|.

Se A e B são pontos do eixo E, com A à esquerda de B, e suas coordena- das respectivas são a e b, então a coordenada x de um ponto arbitrário X do segmento de reta AB é um número x tal que a ≤ x ≤ b. Noutras palavras, ao segmento de reta AB ⊂ E corresponde o intervalo [a, b] ⊂ R.

Parametrização de um segmento.

Para cada ponto X do segmento de reta AB, tem-se evidentemente d(A, X) ≤ d(A, B), logo a razão t = $\frac{d(A, X)}{d(A, B)}$ é um número real compreendido entre 0 e 1. Quando X = A tem-se t = 0 e, quando X = B, vale t = 1.

Se, para cada t ∈ [0, 1], chamarmos de Xt o ponto do segmento de reta AB tal que $\frac{d(A, X_{t})}{d(A, B)}$ = t, veremos que a coordenada $x_{t}$ do ponto $X_{t}$ está relacionada com as coordenadas a e b dos pontos A e B pela igualdade $\frac{x_{t} - a}{b - a}$ = t, ou seja

$x_{t}$ = (1 − t)a + tb = a + t(b − a).

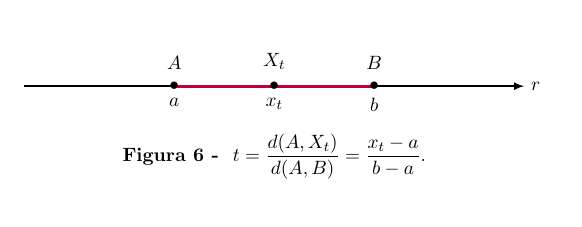
Exemplo 1.

Quando t = $\frac{1}{2}$ o ponto $X_{t}$ = $X_{1/2}$ chama-se ponto médio do segmento AB; sua coordenada

$x_{1/2}$ = $\frac{1}{2}$ a + $\frac{1}{2}$ b = $\frac{a + b}{2}$

é a média aritmética entre as coordenadas a e b dos pontos A e B.

Exemplo 2

Tomando t = $\frac{1}{3}$ , obtemos o ponto X = $X_{1/3}$ cuja coordenada

X = (1 - $\frac{1}{3}$ ) a + $\frac{1}{3}$ b = $\frac{2}{3}$ a + $\frac{1}{3}$ b.

é o número que separa o intervalo [a, b] em dois subintervalos [a, x] e [x, b] com $\frac{x - a}{b - a}$ = $\frac{1}{3}$

Observação 1

Quando estudamos os números reais, fazemos a cada x ∈ R corresponder um ponto X sobre o eixo E. Em Geometria Analı́tica, o processo é inverso: procura-se associar a cada ponto do eixo E um número, chamado sua coordenada. Para isso, admitimos que exista a noção de distância entre dois pontos desse eixo, isto é, que tenha sido fixada uma unidade de comprimento.

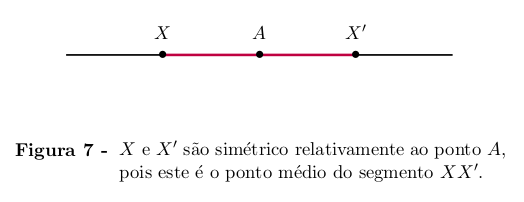
Observação 2

Quando A é o ponto médio do segmento de reta XX', diz-se que X' é o simétrico de X relativamente ao ponto A. Se A, X e X' estão localizados sobre um eixo E e suas coordenadas são respectivamente a, x e x' tem-se então a = $\frac{x + x'}{2}$ , logo x' = 2a − x. Note que desta igualdade resulta x = 2a − x'. Isto corresponde ao fato de que X é por sua vez o simétrico de X' relativamente ao ponto A.

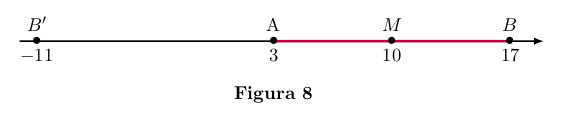
Exemplo 3

Se no eixo E os pontos A e B têm respectivamente coordenadas 3 e 17 então a coordenada do ponto médio do segmento AB é 10 e a coordenada do ponto B', simétrico de B em relação A, é -11.

Coordenadas no Plano

Indica-se como R² o conjunto formado pelos pares ordenados (x, y), onde x e y são números reais.

Dados (x, y) e (x', y') em R² , tem-se (x, y) = (x', y') se, e somente se, x = x' e y = y'. O número x chama-se a primeira coordenada e o número y a segunda coordenada do par (x, y). Observe, por exemplo, que os pares ordenados (2, 3) e (3, 2) são diferentes pois a primeira coordenada de (2, 3) é 2 enquanto que a primeira coordenada de (3, 2) é 3.

Por outro lado, os conjuntos {2, 3} e {3, 2} são iguais pois um objeto pertence a um deles se, e somente se, pertence ao outro. Portanto, um par ordenado não é a mesma coisa que um conjunto com dois elementos. No par ordenado (x, y) pode-se ter x = y mas se {x, y} é um conjunto com dois elementos tem-se necessariamente x ≠ y.

Mostraremos agora como usar R 2 para obter um modelo aritmérico de um plano

Definição (Sistema de coordenadas)

Um sistema de coordenadas (cartesianas) no plano II consiste num par de eixos perpendiculares OX e OY contidos nesse plano, com a mesma origem O. OX chama-se o eixo das abcissas e OY é o eixo das ordenadas. O sistema é indicado com a notação OXY.

A escolha de um sistema de coordenadas no plano II permite estabelecer uma correspondência biunı́voca II → R² . A cada ponto P do plano II fazemos corresponder um par ordenado (x, y) ∈ R² . Os números x e y são as coordenadas do ponto P relativamente ao sistema OXY : x é a abcissa e y é a ordenada de P.

As coordenadas x, y do ponto P são definidas do seguinte modo:

Se P estiver sobre o eixo OX, o par ordenado que lhe corresponde é (x, 0), onde x é a coordenada de P no eixo OX. Se P estiver sobre o eixo OY, a ele corresponde o par (0, y), onde y é a coordenada de P nesse eixo. Se P não está em qualquer dos eixos, traçamos por P uma paralela ao eixo OY, a qual corta OX no ponto de coordenada x e uma paralela ao eixo OX, a qual corta OY no ponto de coordenada y. Então x será a abcissa e y a ordenada do ponto P. Noutras palavras, (x, y) ∈ R² é o par ordenado de números reais que corresponde ao ponto P.

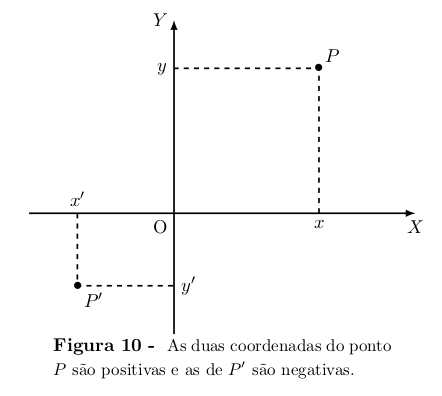
O ponto O, origem do sistema de coordenadas, tem abcissa e ordenada ambas iguais a zero. Assim, a ele corresponde o par (0, 0) ∈ R².

O emprego de coordenadas no plano serve a dois propósitos que se com- plementam. O primeiro é o de atribuir um significado geométrico (e com isto dar um maior conteúdo intuitivo) a fatos de natureza numérica, como o comportamento de uma função real de uma variável real, que ganha muito em clareza quando se olha para seu gráfico. O segundo propósito do uso das coordenadas vai no sentido oposto: recorre-se a elas a fim de resolver problemas da Geometria. Este é o objetivo da Geometria Analı́tica. No primeiro caso, a ênfase recai sobre a corres pondência R² → II e no segundo sobre sua inversa II → R² . Na prática, esses dois pontos de vista se entrelaçam: para estabelecer os fatos iniciais da Geometria Analı́tica usam-se os resultados básicos da Geometria Euclidiana.

Em princı́pio o plano II, cujos elementos são pontos, não é a mesma coisa que o conjunto R² , cujos elementos são pares de números reais. Entre- tanto, quando fixarmos um sistema de coordenadas em II, usaremos a correspondência II → R² para identificar cada ponto P do plano com o par ordenado (x, y) que lhe corresponde. Assim, escrevemos P = (x, y) querendo dizer com isto que P é o ponto do plano cuja abcissa é x e cuja ordenada é y.

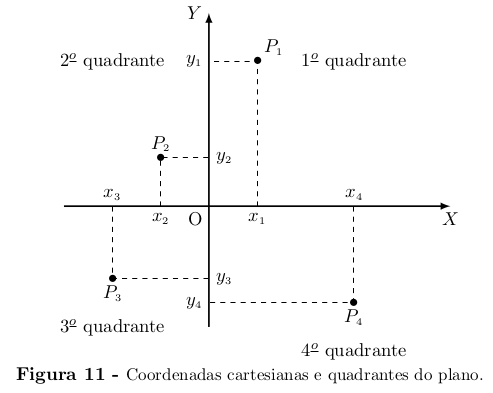
Os eixos ortogonais OX e OY decompõem o plano II em quatro regiões, cada uma das quais se chama um quadrante. O primeiro quadrante é o conjunto dos pontos P = (x, y) tais que x ≥ 0 e y ≥ 0. O segundo quadrante é formado pelos pontos P = (x, y) com x ≤ 0 e y ≥ 0. O terceiro, pelos pontos P = (x, y) com x ≤ 0 e y ≤ 0. Finalmente, os pontos P = (x, y) do quarto quadrante são aqueles em que x ≥ 0 e y ≤ 0.

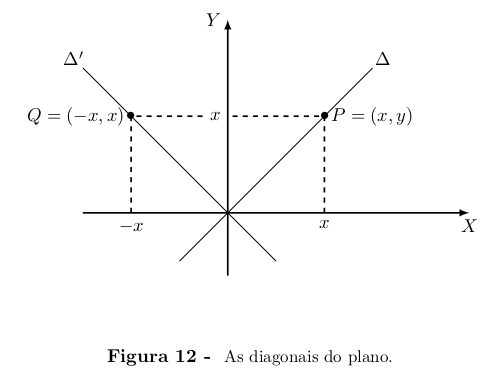
Fixando o sistema de coordenadas OXY no plano Π, o primeiro e o terceiro quadrantes formam dois ângulos retos, opostos pelo vértice. Os pontos P = (x, y) da bissetriz comum desses dois ângulos são (como todos os pontos de uma bissetriz) equidistantes dos lados, logo têm ab- cissa e ordenada iguais (ambas positivas no primeiro quadrante e ambas negativas no terceiro). Esta reta ∆ chama-se a diagonal do plano II (relativamente ao sistema OXY). Tem-se portanto P = (x, y) ∈ ∆ se, e somente se, x = y.

Analogamente, um ponto Q = (x, y) pertence à bissetriz ∆' comum ao segundo e quarto quadrantes se, e somente se, x = −y.

Ponto Médio de um Segmento

Dados os pontos A = (a, b) e A' = (a', b'), quais são as coordenadas do ponto médio M = (x, y) do segmento de reta AA'? A resposta é

x = $\frac{a + a'}{2}$ e y = $\frac{b + b'}{2}$

e a ela chegaremos usando um pouco de Geometria Plana.

Suponhamos inicialmente que a ≠ a' e b ≠ b' , isto é, o segmento AA' não é vertical (paralelo ao eixo OY) nem horizontal (paralelo ao eixo OX). Então, considerando os pontos P = (x, b) e Q = (a', y), vemos que APM e MQA' são triângulos retângulos cujas hipotenusas AM e MA' têm o mesmo comprimento, já que M é o ponto médio de AA'. Além disso, os ângulos agudos PÂM e QMA' são congruentes porque os lados AP e MQ são paralelos. Portanto APM e MQA' são triângulos congruentes.

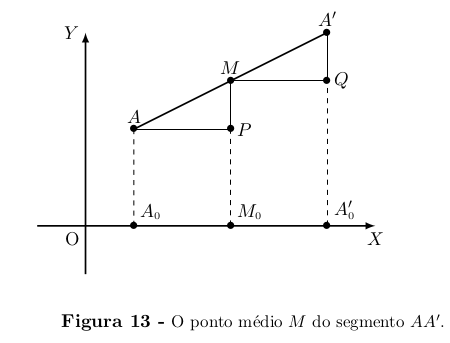
Daı́ resulta que os segmentos AP e M Q têm o mesmo comprimento. Logo, pondo $A_{0}$ = (a, 0), $M_{0}$ = (x, 0) e ${A'}_{0}$ = (a', 0), concluı́mos que $M_{0}$ é o ponto médio do segmento $A_{0} {A'}_{0}$ no eixo OX. Segue-se então que x = $\frac{a + a'}{2}$ . De modo análogo se vê que y = $\frac{b + b'}{2}$ .

Quando o segmento AA' é horizontal (isto é, b = b') ou vertical (a = a'), o argumento acima se simplifica, reduzindo-se imediatamente ao caso do ponto médio de um segmento localizado sobre um eixo.

Exemplo 4

Encontre as coordenadas do ponto médio do segmento AB, onde A = (1, 2) e B = (5, 4).

Solução.

Seja M = (x, y) as coordenadas do ponto médio do segmento AB. Então

x = $\frac{1 + 5}{2}$ = 3 e y = $\frac{2 + 4}{2}$ = 3

Portanto

M(3, 3).

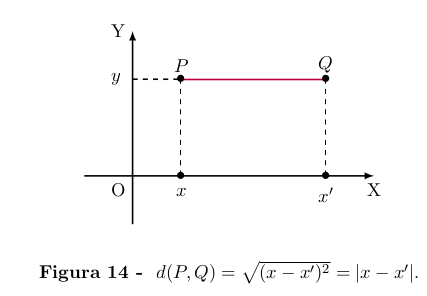
Se os pontos P = (x, y) e Q = (x', y) têm a mesma ordenada y então a distância d(P, Q) entre eles é igual à distância

|x − x'| = $\sqrt{(x - x')²}$

entre suas projeções sobre o eixo OX.

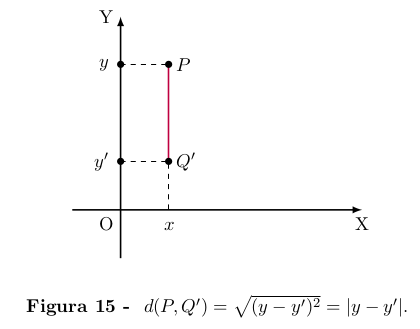
Analogamente, se P = (x, y) e Q' = (x, y') têm a mesma abcissa x então

d(P, Q) = |y − y'| = $\sqrt{(y - y')²}$

que é igual à distância entre as projeções de P e Q sobre o eixo OY.

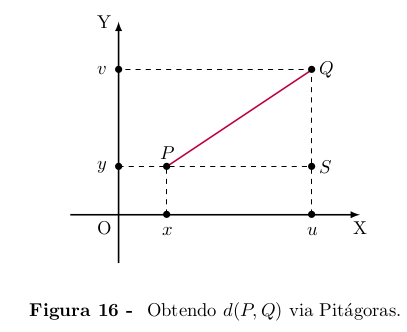
Se, entretanto, P = (x, y) e Q = (u, v) têm abcissas e ordenadas dife- rentes então, considerando o ponto S = (u, y), vemos que P SQ é um triângulo retângulo cuja hipotenusa é P Q. Como P e S têm a mesma ordenada, enquanto S e Q têm a mesma abcissa, segue-se que

d(P, S) = |x − u| e d(S, Q) = |y − v|.

Pelo Teorema de Pitágoras, podemos escrever

d(P, Q)² = d(P, S)² + d(S, Q)².

Portanto,

d(P, Q)² = (x − u)² + (y − v)²,

Logo,

d(P, Q) = $\sqrt{(x - u)² + (y - v)².}$

Em particular, a distância do ponto P = (x, y) à origem O = (0, 0) é

d(O, P) = $\sqrt{x² + y².}$

Exemplo 5

Qual a distância entre os pontos P = (1, 2) e Q = (4, 5)?

Solução

Pela fórmula da distância entre dois pontos, temos:

$\sqrt{(4 - 1)² + (5 - 2)²}$ = $\sqrt{9 + 9}$ = $\sqrt{18}$ = 3 $\sqrt{2}$

Portanto, d(P, Q) = 3 2.
A fórmula da distância entre dois pontos, dada em termos das coordena- das desses pontos, serve de partida para um grande número de resultados da Geometria Analı́tica.

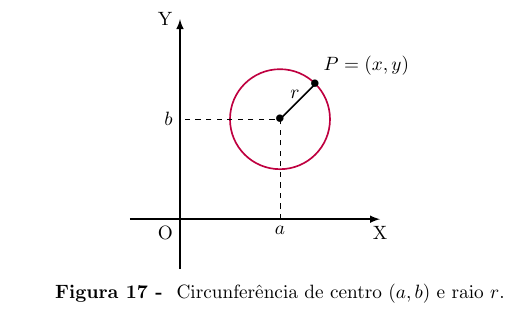
Se o centro de uma circunferência C é o ponto A = (a, b) e o raio é o número real r > 0 então, por definição, um ponto P = (x, y) pertence a C se, e somente se, d(A, P ) = r. Pela fórmula da distância entre dois pontos, vemos que

C = {(x, y); (x − a)² + (y − b)² = r²}.

Diz-se então que

(x − a)² + (y − b)² = r²

é a equação da circunferência de centro no ponto A = (a, b) e raio r.logo

Dados os pontos P = (x, y) e Q = (u, v), qual é a condição, em termos dessas coordenadas, que assegura o perpendicularismo dos segmentos OP e OQ, onde O = (0, 0) é a origem? Pelo Teorema de Pitágoras, os segmentos OP e OQ são perpendiculares se, e somente se,

d(P, Q)² = d(O, P)² + d(O, Q)².

A fórmula da distância entre dois pontos nos permite escrever esta equação como

(x − u)² + (y − v)² = x² + y² + u² + v²,

ou seja:

x² − 2xu + u² + y² − 2yv + v² = x² + y² + u² + v².

Simplificando:

−2ux − 2vy = 0

e daı́

ux + vy = 0.

A igualdade ux + vy = 0 expressa portanto a condição necessária e su- ficiente para que os segmentos OP e OQ sejam perpendiculares, quando O é a origem, P = (x, y) e Q = (u, v).

Dados os pontos O = (0, 0), P = (1, $\frac{2}{3}$ ) e Q = (−2, 3). Os segmentos OP e OQ são perpendiculares, pois

1 x (-2) + $\frac{2}{3}$ x 3 = 0

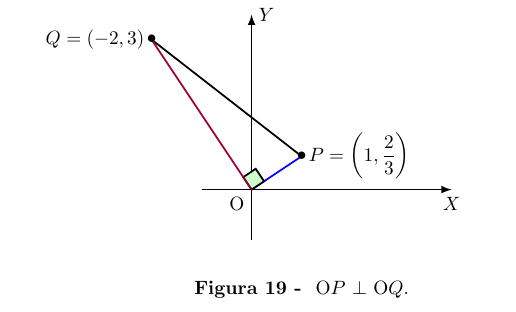
Mais geralmente, sejam A = (a, b), A' = (a' , b'), C = (c, d) e C' = (c', d') com A ≠ A' e C ≠ C'. Qual é a condição em termos dessas coordenadas que assegura serem perpendiculares os segmentos de reta AA' e CC'?

Transladando paralelamente os segmentos AA' e CC' de modo a fazer os pontos A e C coincidirem com a origem O = (0, 0), obtemos os pontos A'' = (α, β) e C'' = (γ, δ) tais que OA'' é paralelo a AA' e OC'' é paralelo a CC'.

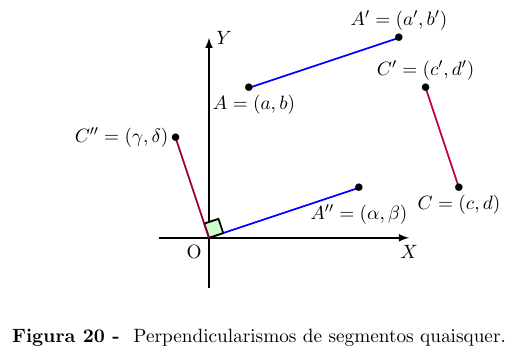
Onde, α = a' − a, β = b' − b, γ = c' − c, δ = d' − d. Além disso, os segmentos AA' e CC' são perpendiculares se, e somente se, OA'' ⊥ OC'', ou seja αγ + βδ = 0.

Assim, a condição de perpendicularismo dos segmentos de reta AA' e CC' se exprime, em termos das coordenadas dos pontos extremos desses segmentos, como

(a' − a) x (c' − c) + (b' − b) x (d' − d) = 0.

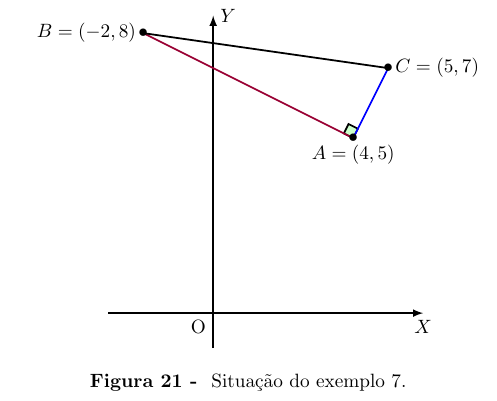
Exemplo 7.

Sejam A = (4, 5), B = (−2, 8) e C = (5, 7). O triângulo ABC é retângulo e seus catetos são AB e AC. Com efeito, os segmentos AB e AC são perpendiculares, pois

(5 − 4) x (−2 − 4) + (7 − 5) x (8 − 5) = 1 · (−6) + 2 · 3 = −6 + 6 = 0.

As Equações da Reta

Uma vez escolhido um sistema de coordenadas no plano, as curvas nesse plano passam a ser representadas por equações. Chama-se equação de uma curva C a uma igualdade envolvendo as variáveis x, y, a qual é satisfeita se, e somente se, o ponto P = (x, y) pertence à curva C.

Exemplo 8.

x = y é a equação da bissetriz comum ao primeiro e terceiro quadrantes, isto é, da diagonal ∆, porque o ponto P = (x, y) pertence a ∆ se, e somente se, x = y. Analogamente, x = −y é a equação da reta ∆', bissetriz comum ao segundo e quarto quadrantes.

Há três tipos principais de equações que definem retas no plano. Trataremos inicialmente da equação y = ax + b.

A equação y = ax + b

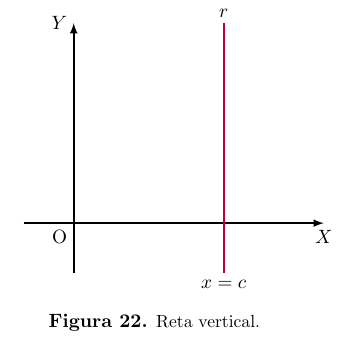
Definição. (Retas verticais)

Diz-se que a reta r é vertical quando ela é paralela ao eixo OY ou coincide com ele.

Se a reta vertical r corta o eixo OX no ponto de abcissa c então todos os pontos de r são da forma P = (c, y) com y ∈ R arbitrário. Diz-se então que a equação da reta r é x = c.

Definicão. (Retas horizontais)

Diz-se que r é horizontal quando é paralela ao eixo OX ou é o próprio OX.